Caching is a process of making frequently used and not often changed data more available and easy to access by placing or copying them at fast accessing and computationally less costly memory space.
The basic working concept of caching is straightforward. If any data is cached, it first looks for data from the faster access memory(where the data is cached). In this case, the application server does not make costly network requests to its database if it is found there. If the cache hit misses, the application server makes a direct request to the database server.
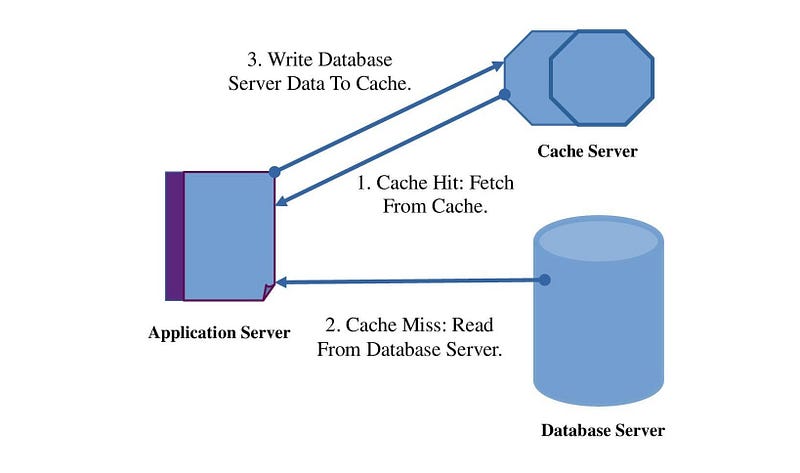
- Faster access to data.
- Reduce computationally costly database server network requests.
- Speed up a slow-performing system.
Let’s Understand Caching With A Scenario:
Suppose, You have a bookshelf and You have plenty of different kinds of books there. Next week is your programming exam. So, You have planned to read only programming-related books. So, instead of finding books each time from the shelf, You can fetch all the programming-related books at a time and put them on Your table. You can pick your needing book from the table. You do not have to waste time fetching a book from the shelf each time. So you get more time to read and concentrate.
Consider, the shelf as the database server, Your table as caching memory, and the programming-related books are your cache. So, keeping those books on Your table, saving your time for going near the shelf and fetching books. Consider going near the shelf and fetching books as network requests to the database server. So, now we understand how caching reduces unnecessary requests to the database and makes a system faster, and increase the efficiency of any system releasing more bit of processor from unnecessary HTTP requests.
To understand the very basics of caching more clearly, a python dictionary based naive example could be like this:
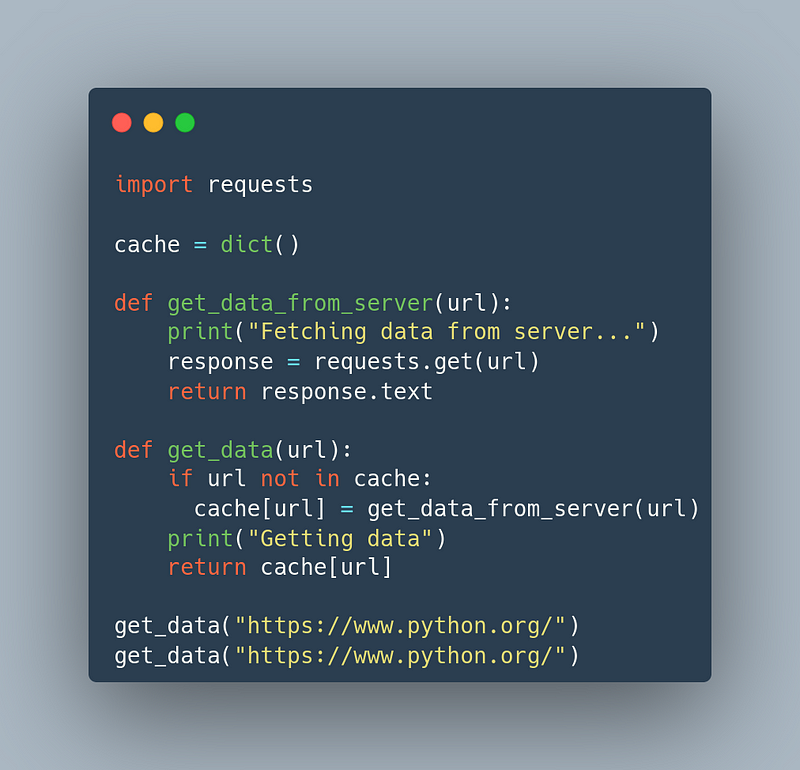
Here in this example, imagine the cache named dictionary as the caching memory. When the get_data function is called, it calls the get_data_from_server function to fetch data from the server for the first time and store data in our cache dictionary. When the get_data function is called for the second time, it does not call the get_data_from_server function to fetch data as there is data in cache and simply take the data from the cache without making costly requests to the server. This is the simple mechanism of caching.

One of the characteristics of caching is the space for caching is limited. And we have to be very selective about the data that we want to cache. We have to know when we should cache data and when we should not.
We will be caching, if-
- Very slow to fetch server data.
- A lot of requests for static data.
- Hardly, changes data.
- To reduce the load on the primary database and balance load.
We will not cache if-
- Takes a lot of time to access data.
- Low repetition of data on requests.
- Frequently changes data.
So, we have learned that cache data should not increase indefinitely. We have to limit the size of cache data. For that, we need to eliminate data from cache memory. Now, the question arises, Which data to keep and which to remove?
To decide on this, there are some policies. These policies are called Cache Eviction Policies.
Cache Eviction Policies:
There are several kinds of cache eviction policies. Some of the most used are-
- Random Replacement(RR)
- Least Frequently Used(LFU)
- Least Recently Used(LRU)
- First In First Out(FIFO)
Let’s take a quick journey to understand these cache eviction policies-
Random Replacement(RR):
From the name, we are getting the idea about RR cache. When it reaches the limit of caching, it just eliminates previously cached data randomly from the cache space. It is not important here, which data is cached first or which data is cached last, or any other parameters. It picks data randomly to eliminate from the cache server to make space for new cache data. Let’s see a demo code for RR-
from cachetools import cached, RRCache
import time
@cached(cache = RRCache(maxsize = 3))
def myfunc(n):
s = time.time()
time.sleep(n)
return (f"Executed: {n}")
s = time.time()
print(myfunc(3))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(3))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(6))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(5))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(6))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(5))
print("Time Taken to execute: ", time.time() - s, "\n")
'''
Result:
Executed: 3
Time Taken to execute: 3.003613233566284
Executed: 3
Time Taken to execute: 0.00010895729064941406
Executed: 2
Time Taken to execute: 2.0036702156066895
Executed: 6
Time Taken to execute: 6.007461309432983
Executed: 5
Time Taken to execute: 5.005535364151001
Executed: 1
Time Taken to execute: 1.0015869140625
Executed: 2
Time Taken to execute: 2.0025484561920166
Executed: 6
Time Taken to execute: 6.006529808044434
Executed: 2
Time Taken to execute: 2.002703905105591
Executed: 1
Time Taken to execute: 0.00014352798461914062
Executed: 5
Time Taken to execute: 5.005505800247192
'''If you look at the executed numbers and observe the time of execution of the numbers, you will understand the RR cache is removing previously cached numbers randomly when the limit for storing numbers is exceeding.
Least Frequently Used(LFU):
LFU keeps the most frequently used data to cache and eliminates less frequently used data if the limit of cache storage exceeds. We can have a clear idea about LFU if we look at the code below-
import time
from cachetools import cached, LFUCache
@cached(cache = LFUCache(maxsize = 3))
def myfunc(n):
time.sleep(n)
return (f"Executed: {n}")
s = time.time()
print(myfunc(3))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(3))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(4))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(5))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(5))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(6))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(4))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(5))
print("Time Taken to execute: ", time.time() - s, "\n")
'''
Result:
Executed: 3
Time Taken to execute: 3.003491163253784
Executed: 3
Time Taken to execute: 0.00011420249938964844
Executed: 1
Time Taken to execute: 1.0017178058624268
Executed: 1
Time Taken to execute: 0.0001633167266845703
Executed: 2
Time Taken to execute: 2.0025696754455566
Executed: 4
Time Taken to execute: 4.004656791687012
Executed: 5
Time Taken to execute: 5.005551099777222
Executed: 5
Time Taken to execute: 0.00011658668518066406
Executed: 6
Time Taken to execute: 6.006593942642212
Executed: 1
Time Taken to execute: 0.0003552436828613281
Executed: 4
Time Taken to execute: 4.004685401916504
Executed: 5
Time Taken to execute: 0.0001475811004638672
'''If we go through the output section of the code we will see, number 1 is used more frequently than number 4, previously. So at last, when we called the function myfunc with 1, it takes no time to execute because, 1 is taken from the cache, but while 4 is called afterward, it takes its execution time to execute as 4 is no longer in the cache while it is called lastly. So, from this scenario, we understand, how the LFU cache keeps more frequently data in the cache and eliminates less frequently used data.
Least Recently Used(LRU):
In LRU policy, the most recent data are kept in cache memory within the limit of caching space. It removes old data in terms of the time of use and makes room for new data. Recently used data remains in the cache.
import time
from cachetools import cached, LRUCache
@cached(cache = LRUCache(maxsize = 3))
def myfunc(n):
# This delay resembles some task
time.sleep(n)
return (f"Executed: {n}")
s = time.time()
print(myfunc(3))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(3))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(4))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(3))
print("Time Taken to execute: ", time.time() - s, "\n")
'''
Result:
Executed: 3
Time Taken to execute: 3.003572702407837
Executed: 3
Time Taken to execute: 0.00012040138244628906
Executed: 2
Time Taken to execute: 2.002492666244507
Executed: 1
Time Taken to execute: 1.0015416145324707
Executed: 4
Time Taken to execute: 4.004684925079346
Executed: 1
Time Taken to execute: 0.0001659393310546875
Executed: 3
Time Taken to execute: 3.0035295486450195
'''Let’s look at the LRU cache code example. We will see that the most recently used data are not taking any time to execute, whereas some data that has been called much earlier is taking its execution time to execute as the data has been removed already by LRU cache policy. Thus, we get the idea of how the LRU cache policy works as an eviction policy keeping recently used data to cache.
First In First Out(FIFO):
FIFO is a method where the first element of the data is processed first and the last element of the data is processed last. So, from the FIFO method, we understand that in the FIFO cache policy, the cache memory will evict the firstly stored cache first and it will keep the newest cache data in the cache memory within the cache limit.
import time
CACHE_LIMIT = 3
fifo_cache = []
def myfunc(n):
if n not in fifo_cache:
time.sleep(n)
fifo_cache.append(n)
if len(fifo_cache)>CACHE_LIMIT:
fifo_cache.pop(0)
return (f"Executed: {n}")
s = time.time()
print(myfunc(3))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(3))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(4))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(5))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
'''
Result:
Executed: 3
Time Taken to execute: 3.003526449203491
Executed: 2
Time Taken to execute: 2.002443552017212
Executed: 3
Time Taken to execute: 0.00011157989501953125
Executed: 1
Time Taken to execute: 1.0014557838439941
Executed: 4
Time Taken to execute: 4.004620790481567
Executed: 5
Time Taken to execute: 5.005484104156494
Executed: 2
Time Taken to execute: 2.0024352073669434
'''In the example, we have simulated a simple FIFO method caching policy. We have declared a cache limit in CACHE_LIMIT variable. When this cache limit exceeds, the caching policy evicts the older data from the cache and keeps the newer data.
Evicting Cache Entries Based on Both Time and Space:
We have seen various kinds of cache eviction policies above. Now we can apply space and time limitation parameters to those policies if we want to manage cache more precisely. These parameters declare a lifetime for every caching data. To do this, we can write our own custom cache decorator function that will consider defined expiry time and evicting space while caching.
import time
from functools import lru_cache, wraps
from datetime import datetime, timedelta
def lru_cache_with_time_and_space_parameter(seconds: int, maxsize: int):
def wrapper_cache(func):
func = lru_cache(maxsize=maxsize)(func)
func.lifetime = timedelta(seconds=seconds)
func.expiration = datetime.utcnow() + func.lifetime
@wraps(func)
def wrapped_func(*args, **kwargs):
if datetime.utcnow() >= func.expiration:
func.cache_clear()
func.expiration = datetime.utcnow() + func.lifetime
return func(*args, **kwargs)
return wrapped_func
return wrapper_cache
@lru_cache_with_time_and_space_parameter(5, 32)
def myfunc(n):
# This delay resembles some task
time.sleep(n)
return (f"Executed: {n}")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(6))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(6))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
'''
Result:
Executed: 2
Time Taken to execute: 2.0024309158325195
Executed: 2
Time Taken to execute: 0.00011897087097167969
Executed: 6
Time Taken to execute: 6.006444454193115
Executed: 6
Time Taken to execute: 6.006414175033569
Executed: 2
Time Taken to execute: 2.0024681091308594
Executed: 1
Time Taken to execute: 1.0027210712432861
Executed: 1
Time Taken to execute: 0.00016355514526367188
'''In the result part of the code, we will see when the time of caching is exceeding, it is erasing all the data it had in the cache.
Python provides a built-in decorator named as TTLCache from cachetools library what provides what we have done with our custom cache decorator. The built-in function keeps the lifetime and space of the cache. For this, we have to define the space and time parameters to it. TTL’s full form is Time to Live. Let’s see an example-
import time
from cachetools import cached, TTLCache
@cached(TTLCache(maxsize=12, ttl=5))
def myfunc(n):
# This delay resembles some task
time.sleep(n)
return (f"Executed: {n}")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(6))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(6))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
'''
Result:
Executed: 2
Time Taken to execute: 2.003089189529419
Executed: 2
Time Taken to execute: 0.0001232624053955078
Executed: 6
Time Taken to execute: 6.006647348403931
Executed: 6
Time Taken to execute: 0.00012040138244628906
Executed: 2
Time Taken to execute: 2.0025570392608643
Executed: 1
Time Taken to execute: 1.000640869140625
Executed: 1
Time Taken to execute: 0.00013566017150878906
'''This TTLCache function is doing the same thing that our custom function has done.
Streamlit Caching:
streamlit library provides more advanced features than the previously described policies. It provides a mechanism that can be used to manage huge cache data, and to play with complex and lengthy computations. Moreover, it can perform at the same time as fetching data from remote storage.
Streamlit is a third-party library. It is not provided with basic python libraries. So you have to configure streamlit to use it. Follow thefollowing instructions to make use of it with python-
- Create a virtual environment, activate it and install
streamlit. You can also installstreamlitglobally withpip install streamlitcommand. - Run your python script with
streamlit run your_python_script_name.py.
Streamlit is a cool third-party tool to manage caching. After running for the first-time it will show you something like this-
It also provides you with a local host and a network host to view your cache data and play with them. How cool is it?

An implementation of streamlit cache with python is provided below-
import streamlit as st
import time
@st.cache(suppress_st_warning=True) # ???? Changed this
def myfunc(n):
# This delay resembles some task
time.sleep(n)
return (f"Executed: {n}")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(6))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(6))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(2))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
s = time.time()
print(myfunc(1))
print("Time Taken to execute: ", time.time() - s, "\n")
'''
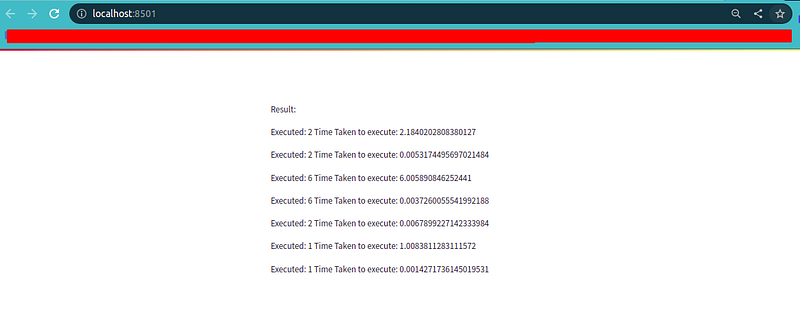
Result:
Executed: 2
Time Taken to execute: 2.1840202808380127
Executed: 2
Time Taken to execute: 0.0053174495697021484
Executed: 6
Time Taken to execute: 6.005890846252441
Executed: 6
Time Taken to execute: 0.0037260055541992188
Executed: 2
Time Taken to execute: 0.0067899227142333984
Executed: 1
Time Taken to execute: 1.0083811283111572
Executed: 1
Time Taken to execute: 0.0014271736145019531
'''To learn more about streamlit caching, You may find streamlit library official documentation helpful.
No cache eviction policy is perfect. A perfect cache eviction algorithm would be if the algorithm can determine which cache data will not be used for the longest period of time in the future. Unfortunately, it is impossible to determine the future lifetime of data when it will be needed. Considering this fact, there is a concept called Bélády’s algorithm. It is the concept of optimal caching policy and it requires future knowledge about data that could determine which data will survive longest in the future and which data will not and determine the future lifetime of data in cache. It is impossible to get the exact future knowledge about data but we can get predictions about the future life of data. For getting this kind of prediction, there have been proposed multiple policies. Some of them are- Hawkeye, Mockingjay, LIRS, ARC, AC, CAR, MQ Etc.

















